Abstract

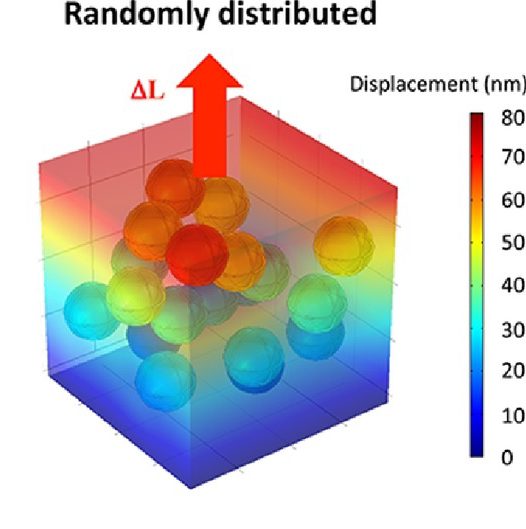
The effective Young’s modulus and Poisson’s ratio of spherical monodisperse and polydisperse core-shell particles ordered or randomly distributed in a continuous matrix were predicted using detailed three-dimensional numerical simulations of elastic deformation. The effective elastic moduli of body-centered cubic (BCC) and face-centered cubic (FCC) packing arrangements of monodisperse microcapsules and those of randomly distributed monodisperse or polydisperse microcapsules were identical. The numerical results were also compared with predictions of various effective medium approximations (EMAs) proposed in the literature. The upper bound of the EMA developed by Qiu and Weng (1991) was in good agreement with the numerically predicted effective Young’s modulus for BCC and FCC packings and for randomly distributed microcapsules. The EMA developed by Hobbs (1971) could also be used to estimate the effective Young’s modulus when the shell Young’s modulus was similar to that of the matrix. The EMA developed by Garboczi and Berryman (2001) could predict the effective Poisson’s ratio, as well as the effective Young’s modulus when the Young’s modulus of the core was smaller than that of the matrix. These results can find applications in the design of self-healing polymers, composite concrete, and building materials with microencapsulated phase change materials, for example.